|
|
|||
| 1. Basic axioms: pitch classes |
Systems of musical analysis are always built upon certain axioms. An axiom is a "given": a statement accepted as true -- in this case for the purpose of developing an analytical method. (Of course, we can always try not accepting an axiom, to see what different analytical insights might result.)
Our introduction to pitch-class set analysis can begin with two underlying axioms.
Axiom 1: Octave equivalence
As in tonal music, the octave seems to play a special role in non-tonal music. Pitches distant from each other by one or more octaves can be treated as equivalent.
We must be clear about what the word "equivalent" means. It does not mean "identical"; pitches an octave apart are different pitches, and a composer would never use one when he means the other. Rather, "equivalent" means "conceptually equal to each other" for the purpose of our analysis.
The axiom of octave equivalence underlies the concept of pitch class (pc): all pitches that are separated by one or more octaves are given the same name and are considered to belong to the same class. This is a familiar concept among musicians. When we speak, for instance, about a piece of music in D major, it's not any particular pitch D that we think of as the tonal centre, but the pitch class D. Notice that pitch class is not itself a primary musical experience -- we hear pitches, not pitch classes -- but a concept abstracted from that experience.
Axiom 2: Enharmonic equivalence
In tonal music, pc A-sharp is not equivalent to pc B-flat; pitches belonging to these two classes appear in different tonal contexts and with different structural meanings. In non-tonal music, however, such differences no longer seem to matter. Here, enharmonically paired pcs usually seem equivalent, and we shall assume such equivalence from now on. Enharmonic equivalence reduces the number of pcs from at least twenty-one (actually more, counting double-sharps and double-flats) to just twelve.
To reflect enharmonic equivalence, we shall give the pcs new names, ones that carry no tonal biases. Using integer notation, we shall simply number the pcs from 0 to 11. You may find that the new names take a bit of getting used to, but they will simplify some of the operations we shall later use in analysis.
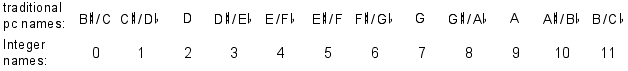
In Example 1-1 this integer notation is used to label the pitch classes
represented in a passage from a song by Webern.
Example 1-1. Anton Webern, "Dies ist ein Lied für dich allein,"
op. 3, no. 1, mm. 4-6. Pitch classes
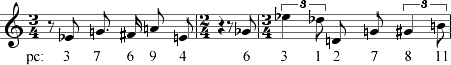
| Exercise 1-1. The integer names of pitch classes |
|
Key concepts on this page:
|
| Page last modified 10 July 2001 / GRT |
|
|||